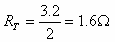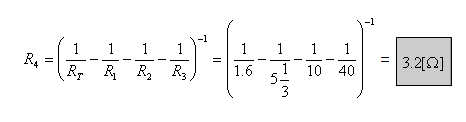קורס בתורת החשמל מאת יוסי יאשי

תרגיל דוגמה 1

נתון מעגל חשמלי כמתואר באיור 3.3:

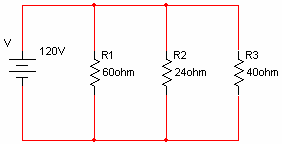
איור 3.3 

חשבו את:

א.       ההתנגדות השקולה ש"רואה" מקור המתח;

ב.       הזרם דרך הנגד R2;

ג.       הזרם היוצא ממקור המתח.

ד.       ההספק המתפתח בנגד .R3

פתרון תרגיל דוגמה 1

א. אפשר לחשב את ההתנגדות השקולה בשתי דרכים:  

דרך אחת – באמצעות הנוסחה:

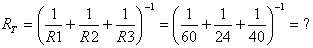
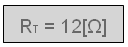
דרך אחרת – באמצעות קירכהוף לזרמים וחוק אום:

בדרך זו, נחשב תחילה את הזרם דרך כל אחד מן הנגדים על פי חוק אום, ולאחר מכן, על פי חוק קירכהוף לזרמים, נחשב את הזרם הכללי.

חשבו את ההתנגדות השקולה באמצעות דרך זו ובדקו את התוצאה הסופית.

ב. נעזר בחוק אום:

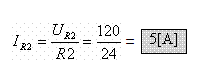
ג. גם את הסעיף הזה אפשר לפתור בשתי דרכים: שימוש בחוק אום או שימוש בחוק קירכהוף לזרמים.

על פי חוק אום:

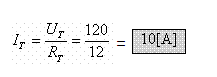
חשבו את הזרם הכללי תוך שימוש בחוק הזרמים של קירכהוף ובדקו את התוצאה הסופית.

ד. יש כמה נוסחאות לחישוב הספק בנגד. במעגלים מקביליים, בגלל שהמתח שווה בכל המעגל, מומלץ השימוש בנוסחה:

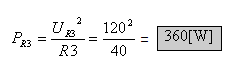
תרגיל דוגמה 2

עשרים נגדים זהים מחוברים במקביל למקור מתח  של 200v. מקור המתח מספק זרם בשיעור של A4. חשבו את:

א.       ערך כל נגד.

ב.       ההספק הכללי במעגל.

פתרון תרגיל דוגמה 2

א. מנתוני השאלה אפשר למצוא באופן ישיר את הנגד השקול של המעגל:

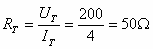
מאחר שהנגדים שחוברו במקביל זהים, אפשר להיעזר בנוסחה 3.4:

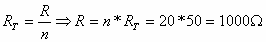
ב. חישוב ההספק הכולל:

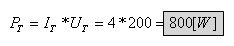
מתשובות לשאלות אלה ניתן להסיק:

במעגל מקבילי המכיל n נגדים זהים מתקיים:

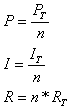
תרגיל דוגמה 3

ההספק הכללי במעגל הנתון באיור 3.4 הוא [W]600.

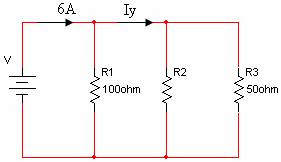
 איור 3.4

חשבו את:

א.       מתח המקור

ב.       ערכו הנגד R2

ג.       הזרם Iy

ד.       מהו המטען המסופק על ידי מקור המתח במשך שעתיים?

פתרון תרגיל דוגמה 3

א. בבואנו לפתור תרגילים מסוג זה, שחסרים בהם נתונים, נתמקד תחילה באותם רכיבים שיש לנו עליהם לפחות שני נתונים. בתרגיל שלפנינו, יש לנו שני נתונים על הנגד השקול. לכן:

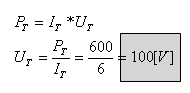
הערה:

אחד הנתונים שתמיד נשאף לחשבו במעגל מקבילי (גם אם לא נדרשנו בשאלה), הוא מתח המקור. הסיבה היא כמובן שמתח זה שייך לכל אחד מהנגדים (תכונה מספר 1 של המעגל המקבילי).

ב. בשלב זה לא נוכל לחלץ את ערכו של R2 על פי חוק אוהם, כיוון שיש ברשותנו מידע רק על המתח שעל פניו.

לו היינו יודעים את ערכו של הנגד השקול, היה אפשר לחשב את ערכו של R2.

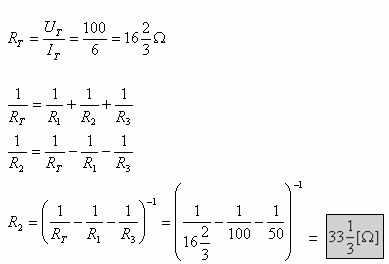
אפשר להגיע לערך הנגד R2 גם בעזרת חוק קירכהוף לזרמים:

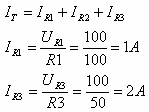
ג. את הזרם Iy נחשב בעזרת חוק הזרמים של קירכהוף:

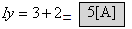
גם אם נרכיב משוואת קירכהוף לזרמים בצומת שלפני, נקבל כמובן אותה תוצאה:

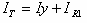
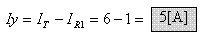
ד. ראשית, נבטא את משך הזמן  בשניות ורק לאחר מכן נחשב את המטען:

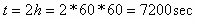
בענף הראשי זורם TI ולכן:

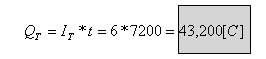
מחברים נגד נוסף במקביל למקור המתח במעגל שמתואר באיור 3.4 רשמו מה יקרה למתח המקור, להתנגדות השקולה, להספק הכללי, לזרם הכללי, למטען הכללי, לאנרגיה הכללית:

תרגיל דוגמה 4

נתון המעגל שבאיור 3.5:

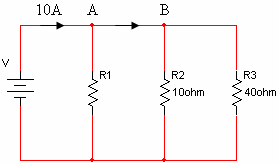
איור 3.5

במוליך AB עובר מטען בשיעור של  [C]1,200 במשך 5 דקות.

חשבו את:

א. ערכו של הנגד R1;

ב.       מתח המקור;

ג.       ערך הנגד שיש לחבר במקביל למעגל, כך שההספק הכללי יגדל פי 2.

פתרון תרגיל דוגמה 4

א. ראשית נחשב את עוצמת הזרם במוליך AB:

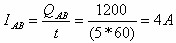
כעת נעזר בחוק קירכהוף לזרמים:

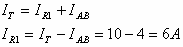
בשלב זה אי אפשר להמשיך, כיוון שאין נגד במעגל (כולל הנגד השקול), שיש לנו עליו שני נתונים.

במצב כזה, יש לנסות לצמצם רכיבים במעגל כדוגמת צמצום הנגדים R2 ו- R3. נחליף את שני הנגדים האלה בנגד אחד שקול שיקרא 2,3R: 

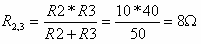
המעגל שווה הערך שיתקבל ייראה כך:

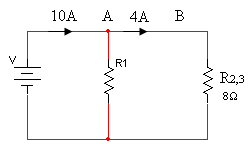
כלומר, על הנגד השקול 2,3R אנו כן יודעים שני נתונים ויכולים לחשב את מפל המתח עליו. מתח זה הוא כמובן מתח המקור (תכונה מספר 2 במעגל המקבילי). 

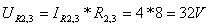
תשובה לסעיף ב: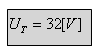     

כעת אפשר לחשב את ערך הנגד R1:

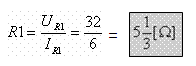
נשתמש בנוסחה 3.2 לחישוב ההתנגדות השקולה במעגל החדש (כתוצאה מהוספת הנגד):

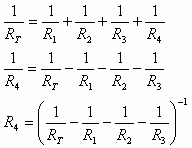
נחשב את הערך החדש של ההתנגדות השקולה לפני הוספת הנגד:

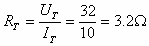
לאחר הוספת הנגד ההתנגדות השקולה קטנה פי 2:

•   הקודם                                                                                                                             
• המשך